6.2 NORMAL PATH quadratic formulas 

Theory

Quadratic formulas are formulas who have a squared letter  (a number multiplied by itself).  Those formulas are used to calculate things in a fast and  easy way. 

 

Those are example of  how  quadratic formulas look like: 

  • y = 5x2 + 2
  • y =  a2
  • b=3c2 

 

You also need to know how to calculate with those kind of formulas.

Example

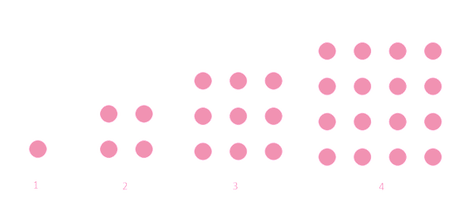
squares, math, mathematics, 6.1 squares

The picture above shows a sequence of dotted squares, you can extend the sequence. 

 

If you are going to count the dots, this will be the results:

  • Shape 1:  1 dot.
  • Shape 2: 4 dots
  • Shape 3: 9 dots
  • Shape 4: 16 dots 

 

You can also calculate the amount of dots by multiplying the length by the width (area square). 

  • Shape 1: 1 . 1 = 12 = 1
  • Shape 2: 2 . 2 = 22 = 4
  • Shape 3: 3 . 3 = 32 = 9
  • Shape 4: 4 . 4 = 42 = 16

Conclusion: You can see that  you can calculate the amount of dots by squaring the number of the shape.

So, the formula of the amount of dots, called n, and the number of the shape, called s, is: 

n = s2 

If you want to know how many dots shape 9 consists of the formula will be: n = 92 = 81 dots. So, shape 9 has 81 dots.

Exercises 

  • Exercise 1:

Given the formula y = -x2 

a) Calculate y for x = 3

b) Calculate y for  x = -4

 

  • Exercise 2:

Given the formula Q = -( 2l + 4 )2

a) Calculate Q for l = 1 

b) Calculate Q for l = -3 

c) Calculate l for Q =  -144

  • Exercise 3: 

Robin is playing tennis. For one of his serves the height h of the ball is given by the formula: 

h = -0.1d2 + 1.2

where h is the height in meters and d the distance in meters.

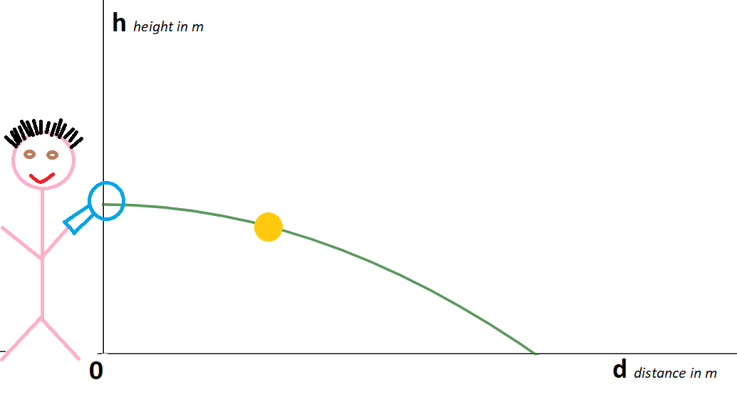
a) Calculate the height of the ball for d= 2

b) What is the height of the ball at the start? 

c) At what distance does the ball hit the floor?