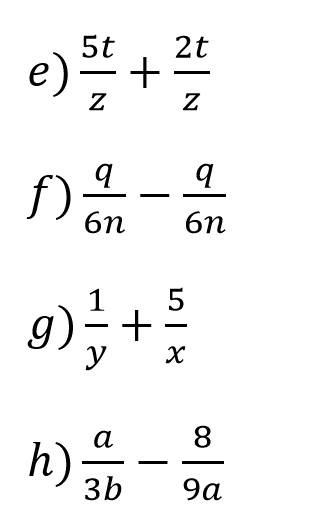6.6 SUPPORTING PATH simplifying algebraic fractions
Theory
Simplifying algebraic fractions
Two-fifth is an example of a fraction. The 2 is called the numerator and the 5 is called the denominator.

You've already learned how to simplify fractions with numbers only. For example simplifying three-sixth: Divide the numerator and denominator by 3. You will get one-second.

The same works with letters, you always have to divide the numerator and the denominator with the same number and/or letter. Look at the example below.
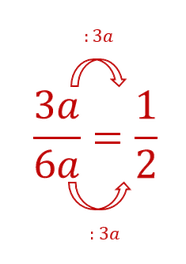
Adding fractions
You have already learned that you may add and subtract fractions with a common denominator. This means that the fractions must have the same denominator before you can add or subtract them.
Two fractions with a common denominator:
Two fractions with a different denominator:
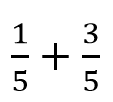
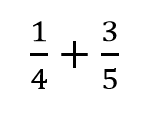
You can always make denominators the same by multiplying the numerator and the denominator of the fractions with the same number. You only need to do this if you have fractions without a common denominator. You need to do exactly the same with fractions with letters, this will be shown in the example.
Examples
Simplifying fractions (numbers only)
As you can see in the theory, you can simplify fractions. However you need to do the same with the numerator and with the denominator otherwise you will get a complete different fraction.
Example:

There are six pieces left of the pie with eight pieces.
In mathematical language: There are six-eighth pieces left.


There are three pieces left of the pie with four pieces.
In mathematical language: There are three-fourth pieces left.
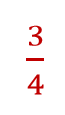

We have now simplified the first pie with a total of 8 pieces to a pie with 4 pieces. If we change the denominator by dividing. We need to change the numerator as well. Otherwise we won't have the same pieces left.
In this case we divided the denominator and the nominator by 2.
Simplifying algebraic fractions (with letters)
The same as with fractions with only numbers, you can simplify fractions with letters. You may only simplify those fractions by dividing the numerator AND the denominator by the SAME letter.
Simplify.
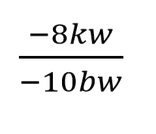
Remember: negative divided by negative equals positive.
We can divide everything by 2 and by w.
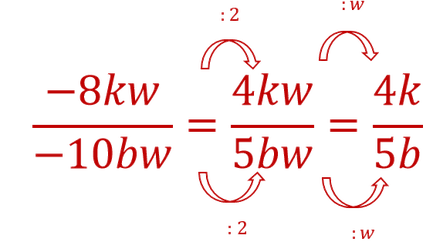
Adding fractions with a common denominator
*NUMBERS ONLY*
You may only add (and subtract) fractions if they have a common denominator. This means that the denominators must be the same.
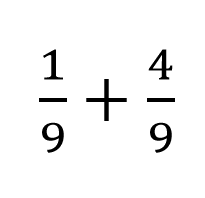
In this case the denominator of both fractions is 9. This means that we are allowed to add the fractions.
With adding (and subtracting) fractions you may only add the numerators.

The explanation of only adding (or subtracting) the numerators while the denominators stay the same is easier when you imagine having two birthday cakes. You are going to cut the two birthday cakes into 9 equal pieces. Each visitor coming to your party may choose which birthday cake he/she likes.


one visitor prefers the pink birthday cake, so you are going to give him/her one of the nine pieces of the pink birthday cake.
four visitors prefer the American birthday cake, so you are going to give them together four out of nine pieces of the American birthday cake.
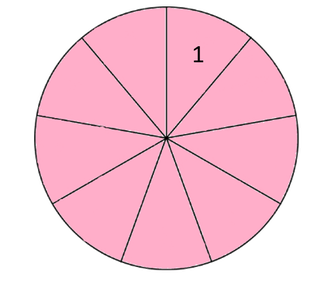
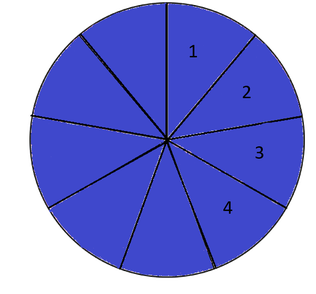
If you want to know how many pieces of pie your visitors ate together, you need to add the pieces of the blue pie and the pink pie. Together it makes five pieces out of a pie of 9 pieces. This is how you will get the answer.

*LETTERS AND NUMBERS MIXED*
Adding fractions with a common denominator and with letters works exactly the same as with fractions with only numbers. The only difference is that there are letters in your fraction. An example is shown underneath.
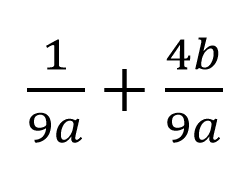
We can see that the denominators in this example are the same, they are both 9a. The only think that we need to take in mind is that we are only allowed to add like terms. 4b and 1 are non like terms so, we may not add them. We may put them together in one numerator, as long as we don't add them.
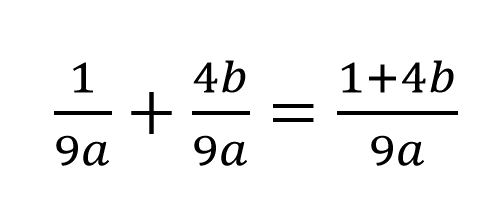
Adding fractions without a common denominator
* NUMBERS ONLY*
Sometimes you will have fractions without a common denominator. If you need to add them, you must make the denominators the same. You can do this with multiplication.
An example of how you can do this is shown below:
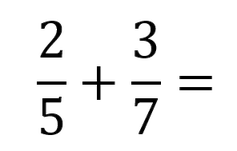
TIP: If you can't immediately see which common number the denominators could be, it is easy to multiply them with each other so, 5 . 7 = 35. This means that the common denominator could be 35.
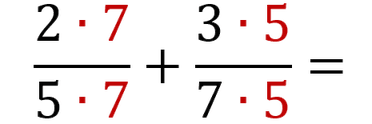
You need to multiply the denominator and the numerator of the same fraction with the same number.
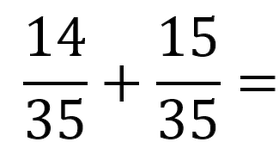
The denominators are the same now, so you may add the fractions!
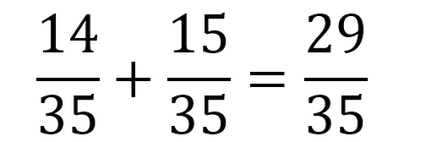
Always check of you can simplify your answer, in this case that isn't possible so this is your final answer.
*LETTERS AND NUMBERS MIXED*
It is also possible that you get fractions without a common denominator but with letters. Again, you need to do exactly the same as with numbers only, you need to make the denominators the same in order to subtract or add the fractions.
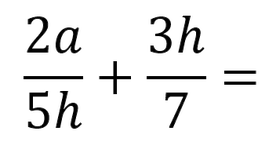
Multiply the numerator and the denominator of the same fraction with the same number in order to make the denominators the same.
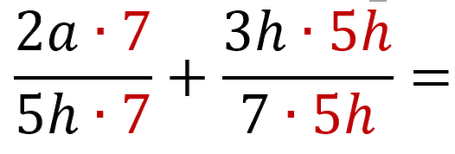
Reminder: 3 . 3 = 32 , x . x = x2 so, h . h = h2
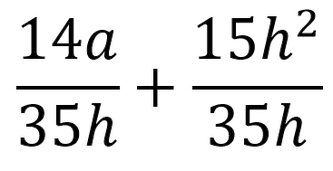
The denominators are the same now, you may add (or subtract) the two fractions.
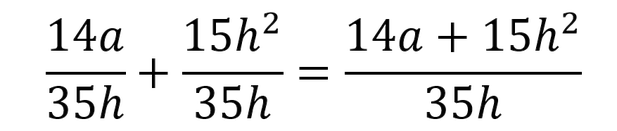
You may only add or subtract like terms! Always check if you can simplify your final answer.
Exercises
Simplify