6.1 SUPPORTING PATH squares
Theory
Squares are 2-D shapes because they are flat. The characteristics of squares are that they have 4 edges which are equally long. They also have 4 right-angles (90 degrees). You can see this in the picture below.


You can calculate the area of a square by using the following formula:
Area square = length x width
Exercise area square:
Calculate the area of the given square.

A squared number is a number multiplied by itself.
An example of a squared number is 52 = 25, this is the same as 5 . 5 = 25 .
Another example is 32 = 9, this is the same as 3 . 3 = 9.
A square root is the opposite of a squared number.
An example of this is √25 = 5, because 52 = 5 . 5 = 25
Another example is √9 = 3, because 32 = 3 . 3 = 9
The square of a square root (√...)2
( √5 )2 = √5 . √5 = √25 = 5
( √7 )2 = √7 . √7 = √49 = 7
You can also simplify square roots using multiplication:
√500 = √(5 . 100) = √5 . √100 = √5 .10 = 10√5
√32= √(16 . 2) = √16. √2= √2 . 4 = 4√2
Examples
Squares
You have just seen that when you are calculating the area of a square you need to multiply the length of the edges by itself. In the exercise above you did 8 . 8 = 64.
A shorter way to write a number multiplied by itself is 82 this is exactly the same as 8 . 8.
So, a number multiplied by itself is called a squared number.

A couple of examples:
- Instead of writing down 5 . 5 = 25 we can write down 52 = 25, this is a shorter way.
52 is the same as 5 . 5
32 is the same as 3 . 3
262 is the same as 26 . 26
we call the ...2 a squared number. 52 is five squared, 32 is three squared and 262 is twenty-six squared.
- You can also write the square numbers of negative numbers. Pay attention between the difference of negative numbers with and without brackets.
With brackets
(-5)2 is the same as -5 . -5 = 25
(-3)2 is the same as -3 . -3 = 9
You do square the minus sign
(-26)2 is the same as -26 . -26 = 676
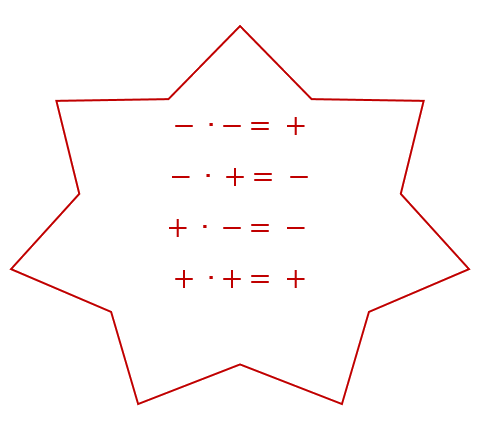
Without brackets
-52 is the same as -5 . 5 = -25
-32 is the same as -3 . 3 = -9
You don't square the minus sign
-262 is the same as -26 . 26 = -676
Square roots
A square root (√) is the opposite of a square.
√25 = 5 because 5 . 5 = 52 = 25
√9 = 3 because 3 . 3 = 32 = 9
√676 = 26 because 26 . 26 = 262 = 676

!!You can not take the square root of a negative number because there is not a squared number where the answer has a negative outcome!!
Example:
- √-16 = no answer
Because 4 . 4 = 42 = 16 --> not -16
-4 . -4 = (-4)2 = 16 --> not -16
So, the answer will never be -16 and that's why there is no answer (n.a.) of a square root with a negative number.
- -√16 = -4
Because the -1 in front of the square root is actually a invisible -1 multiplied by the square root. You will get the following calculation:
= -1 . √16
= -1 . 4
= -4
The square of a square root √..2
You already know that opposite of squaring a number is taking the square root of a number.
So, √81 = 9 because 92 = 9 . 9 = 81
But, what happens if we square a square root?
Examples:
( √9 )2 = √9 . √9 = √81 = 9
( √9 )2 = ( 3 )2 = 9
( √4 )2 = √4 . √4 = √16 = 4
( √4 )2 = ( 2 )2 = 4
( √5 )2 = √5 . √5 = √25 = 5
( √7 )2 = √7 . √7 = √49 = 7
You can see that the answer of the square root squared is equal to the number underneath the square root. A square and a square root cancel each other out.
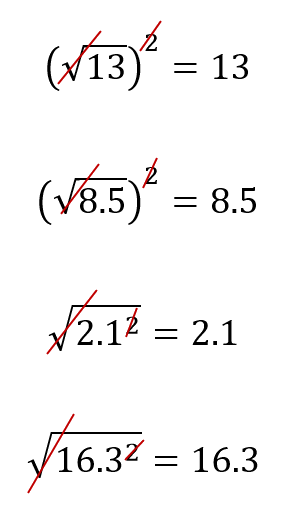
Exercises
- Exercise 1
Calculate
a) 62
b) (-10)2
c) -92
d) 42 + 3 - 1
e) 62 - 32
f) (7 - 6)2
g) (1/4)2 + (2/3)2
h) 7 - 62 : 3
- Exercise 2
Calculate
a) (-8)2
b) √81
c) -√121
d) √-144
e) √49 + 42 - 1
f) 3 . √121 + 7 . √625

