6.2 ANSWER supporting path
Answers exercises
- Exercise 1
Given the formula y=x2 + 1
a) Calculate y for x = 3
Step 1: Fill x = 3 into the formula
y = 32 + 1
Step 2: Calculate the formula
y = 9 + 1
y = 10
b) Calculate y for x = -3
Step 1: Fill x = -3 into the formula
y = (-3)2 + 1
Step 2: Calculate the formula
y = 9 + 1
y = 10
c) Calculate x for y = 26
Step 1: fill y = 26 into the formula
26 = x2 + 1
Step 2: Numbers to one side and letters to one side
25 = x2
Step 3: Take the square root
√25 = x
x = 5


- Exercise 2:
Given the formula B = 4.1a2 + 2
a) Check that B = 20.081 when a = 2.1
Step 1: Fill a = 2. 1 into the formula.
B = 4.1 . 2.12 + 2
B = 4.1. 4.41 + 2
B = 18.081 + 2 = 20.081
b) Check that B = 5.321 when a = -0.9
Step 1: Fill a = -0.9 into the formula.
B = 4.1 . (-0.9)2 + 2 =
B = 4.1 . 0.81 + 2
B = 3.321 + 2 = 5.321
c) Tim picks a number for a and gets B = 412.
Which numbers could he have uses for a?
Step 1: Fill B = 412 into the formula.
412 = 4.1a2 + 2
Step 2:
- Exercise 3:
Robin is playing tennis. For one of his serves the height h of the ball is given by the formula:
h = -0.1d2 + 1.2
where h is the height in metres and d the distance in metres.
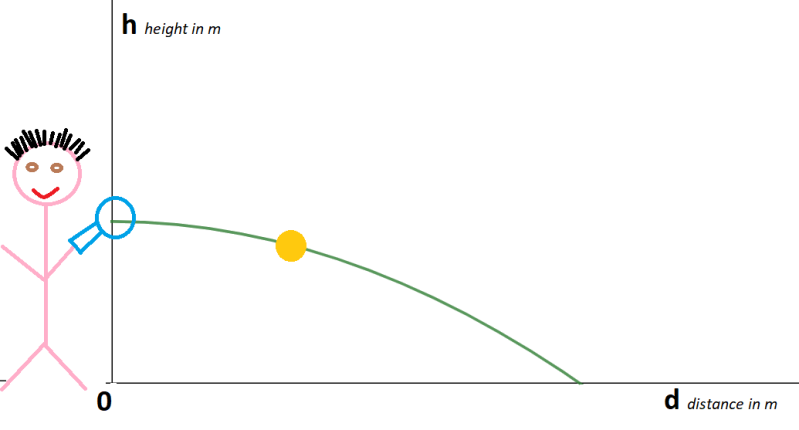
a) Calculate the height of the ball for d= 2
h = -0.1d2 + 1.2
d= 2 so, fill it in.
h = -0.1 . 22 + 1.2
h = -0.1 . 4 + 1.2
h = -0.4 + 1.2 = 0.8 m
So, the height of the ball at a distance of 2 meters is 0.8 meters.
b) What is the height of the ball at the start?
Two methods:
- The height of the ball at the start is 1.2 meters. You can see this immediately because 1.2 is the starting point.
or
- To know the height of the ball at the start you have to fill in 0 for d because that's where you start.
h = -0.1. 02 + 1.2 = 1.2 meters
so, the height of the ball at the start is 1.2 meters.
c) What is the height of the ball when it hits the floor?
The ball hits the floor when the height is equal to zero. That's when h = 0.
d) At what distance does the ball hit the floor?
The ball hits the floor when the height is equal to zero. That's when h = 0, fill this into your formula. 0 = -0.1d2 + 1.2
Two methods:
- Step 1: All numbers to one side and all letters to the other side.
0.1d2 = 1.2
Step 2: Divide by the number before the letter
d2 = 12
Step 3: Take the square root to get rid of the squared
d = √12 ≈ 3.5 meters
Step 4: Conclusion
So, at 3.5 meters the ball will hit the floor.
or
- You may also find d2 = 12 by trying, afterwards you still have to take the root and give a conclusion.



